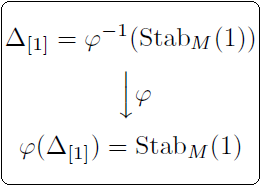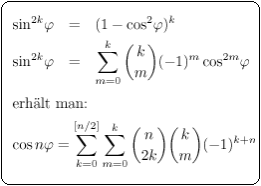Patrick Reichert

Publikationen

Nennerfreie Gleichungen für elliptische Kurven mit Torsionspunkt der Ordnung 4 bis 20 (Juni 2017)

Beschreibung: Die von Andrew Sutherland optimierten Darstellungen elliptischer Kurven vorgegebener Torsion werden so umgeformt, dass die Koeffiziententerme nennerfrei sind. Es wird ein Algorithmus angegeben, der eine möglichst kompakte Faktorisierung der Diskriminante in nicht-faktoriellen Polynomringen bestimmt.

Stichworte: Elliptische Kurven, Torsionspunkt, Polynomringe, SAGE

Zugehörige Dokumente:

• Artikel Nennerfreie Gleichungen für elliptische Kurven mit Torsionspunkt der Ordnung 4 bis 20 (Juni 2017)

Bestimmung von Weil-Funktionen auf elliptischen Kurven (Juli 2016)

Beschreibung: Für n ∈ {4, ..., 10, 12} wird für jede elliptische Kurve (E, O) mit n-Torsionspunkt P = (0,0) ∈ E die Gleichung der Weil-Funktion bestimmt, also der meromorphen Funktion f:E → C ∪ {∞} mit Divisor n[P]-n[O]. Die berechneten Funktionen werden mit Hilfe der charakteristischen Eigenschaft f(Q) f(-Q) = (-1)ⁿ xⁿ für alle Punkte Q=(x,y) ∈ E zusätzlich verifiziert.

Stichworte: Elliptische Kurven, Torsionspunkt, Weil-Funktion, Divisor, Miller-Algorithmus, SAGE

Zugehörige Dokumente:

• Artikel Bestimmung von Weil-Funktionen auf elliptischen Kurven (Juli 2016)
• SAGE-Bibliothek zur Bestimmung von Weil-Funktionen als HTML, SAGE-Notebook, SAGE-MarkDown (Juli 2016)
• SAGE-Datenbank mit den berechneten Weil-Funktionen als HTML, SAGE-Notebook, SAGE-MarkDown (Juli 2016)
• Textdatei mit den Weil-Funktionen (Juli 2016)

Eine rationale und eine elliptische Kurve für A₅ (März 2016)

Beschreibung: Für die zwei Beispiele Δ(3,3,5) → A₅ und Δ(3,5,5) → A₅ werden die Gleichungen der Riemannschen Flächen vom Geschlecht 0 und 1 und zugehörige Belyi-Funktionen bestimmt.

Stichworte: Dreiecksgruppe, elliptische Kurve, Riemann-Hurwitz-Theorem

Zugehörige Dokumente:

• Artikel Eine rationale und eine elliptische Kurve für A₅ (März 2016)
• Vortrag Weil-Funktionen und Dessins in Würzburg (September 2009)
• Vortrag Galois-Konjugation Riemannscher Flächen in Magdeburg (Januar 2009)

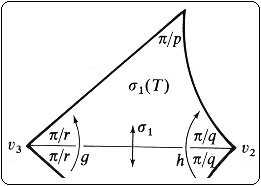
Diplomarbeit: Alternierende Faktorgruppen Fuchsscher Dreiecksgruppen (Dezember 2003)

Beschreibung: Diese Diplomarbeit behandelt eine Fragestellung aus einem Arbeitsgebiet, das erst in den letzten zwanzig Jahren entstanden ist und Querverbindungen zwischen Begriffen wie Uniformisierungstheorie, Fuchssche Gruppen, Riemannsche Flächen, Grothendiecks Dessins d'enfants (Kinderzeichnungen), Teichmüllerräume und sogar Inverse Galoistheorie herstellt.
Herausgegriffen wurde ein Problem, für welches Prof. J. Wolfart von der Johann-Wolfgang-Goethe-Universität Frankfurt/M. im Herbst 2001 meine Aufmerksamkeit weckte. Es sollte die Fragestellung untersucht werden, welche Fuchsschen Dreiecksgruppen alternierende Faktorgruppen besitzen.
Dabei stellte sich recht schnell heraus, dass die Untersuchungen in der Literatur zu dieser Fragestellung bisher vor allem Existenzaussagen lieferten, die für jede Fuchssche Gruppe beispielsweise die Existenz einer Schranke N garantieren, so dass für alle n > N stets ein Epimorphismus in die alternierende Gruppe A_n existiert.
Ganz außer Acht gelassen wurden dabei meist kleine Beispiele und weiterführende Fragestellungen dazu. In dieser Diplomarbeit werden Methoden entwickelt, die es erlauben, in Fuchsschen Dreiecksgruppen effizient zu rechnen. Weiterhin wird am Beispiel einer konkreten Dreiecksgruppe gezeigt, wie entschieden werden kann, ob die Kerne von Epimorphismen in dieselbe alternierende Gruppe in der Gruppe PSL(2, R) zueinander konjugiert sind. Diese Aufgabenstellung korrespondiert also mit dem Wunsch, zueinander nicht isomorphe Riemannsche Flächen mit derselben alternierenden Automorphismengruppe zu finden, die einen vorgegebenen Verzweigungstyp besitzen.
Im ersten Kapitel wird eine Einführung in diese Fragestellungen gegeben, außerdem ist eine ausführliche Literatursicht angefügt. Das zweite Kapitel zeigt allgemeine Eigenschaften der alternierenden Gruppen auf, die anschließend zur Entwicklung von Methoden verwendet werden, alternierende Faktorgruppen für eine vorgegebene Dreiecksgruppe zu finden.
Das dritte Kapitel ist das umfangreichste. Es wird eine Darstellung von Dreiecksgruppenelementen hergeleitet, die es ermöglicht, effizient Berechnungen auf dem Computer durchführen zu können. Im vierten Kapitel wird das Hauptresultat dieser Ausarbeitung bewiesen. Es wird die Existenz von zwei zueinander nicht isomorphen Riemannschen Flächen gezeigt, die beide mit Hilfe von Normalteilern der (3,5,5)-Dreiecksgruppe erzeugt werden und dieselbe Automorphismengruppe A₅ besitzen.

Stichworte: Hyperbolische Geometrie, Arithmetische Dreiecksgruppen

Zugehörige Dokumente:

• Diplomarbeit (Dezember 2003)
• Hauptergebnisse in Englisch (Januar 2006)
• Vortragsfolien zum Workshop Belyi Maps and Dessins on Riemann Surfaces in Frankfurt (April 2006)
• Vortrag in Magdeburg (März 2008)

Beweis eines Satzes über algebraische Zahlen (April 1996)

Beschreibung: Diese Facharbeit wurde in der zehnten Klasse im April 1996 am Georg-Cantor-Gymnasium Halle eingereicht. Das Hauptresultat der Arbeit ist: Wenn cos x algebraisch ist, dann ist auch cos (rx) algebraisch für alle rationalen r.

Stichworte: Eigenschaften algebraischer Zahlen, Formel von Moivre

Zugehörige Dokumente:

• Facharbeit (April 1996)